In the fall of 1982, Billy Joel’s 52nd Street was among the first 50 albums released as consumer-available compact discs. It had been only about four years since digital recording equipment was introduced to studios. This marked a revolutionary change in how consumers would buy their music. It was the dawn of an all-digital era, where performers could have their music captured with impressive accuracy and minimal background noise for delivery to consumers. Since then, not much has changed in the way we digitally capture and store analog waveforms. We just have a few more bits of depth to improve noise performance and higher sampling rates to ensure that bats and mice can hear that extra octave.
On the reproduction side of things, dozens of companies have made claims about increases in performance because of these higher sampling rates and increased bit depth. Unfortunately, the marketing guys haven’t been talking to the engineers to understand how the process works. This article will look at the digital stairstep analogy and explain why it’s misleading.
How Is Analog Audio Sampled?
Digital audio sampling is a relatively simple process. An analog-to-digital converter (ADC) measures the voltage of a waveform at a specific rate and outputs digital information that represents those amplitudes. The sampling rate defines the number of samples per second, determining the Nyquist frequency. The Nyquist frequency is the highest frequency the ADC can record accurately and is half the sample rate. For a compact disc with a sampling rate of 44.1 kHz, the highest frequency is 22.05 kHz. This frequency is beyond what most humans can hear, so it’s more than high enough to capture any audio signal we’d need to reproduce.
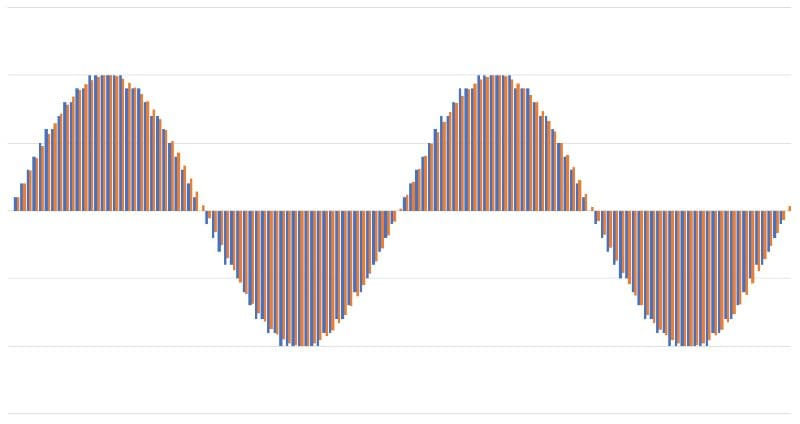
Bit depth describes the number of discrete amplitudes captured in a sampling process. If you have read audio brochures or looked at websites, you’ve undoubtedly seen a drawing showing several cubes intended to represent samples of an analog waveform. These diagrams are often referred to as stairstep drawings.

The size of the blocks on the horizontal scale represents the sampling rate, and the size on the vertical scale is the bit depth. We have 20 levels in this simulation, equating just over 4.3 bits of resolution. It’s not difficult to see that this would introduce some amount of error and unwanted noise. However, even the earliest digital samplers, like the Fairlight CMI, had only 8 bits of depth, equating 256 possible amplitudes. Later versions increased the bit depth to 16, dramatically improving sample accuracy.
Once we have enough bit depth, we can accurately reproduce the waveform without adding unwanted noise. For example, the orange data in the image below has lots of bit depth, and the difference between the orange and blue would be perceived as noise in the recording.
What about those steps? Isn’t music supposed to be a smooth analog waveform and not a bunch of steps? Companies that purport to offer support for higher resolution audio files or those with more bit depth will often put a second image beside the first with smaller blocks. The intention is to describe their device as being more accurate.
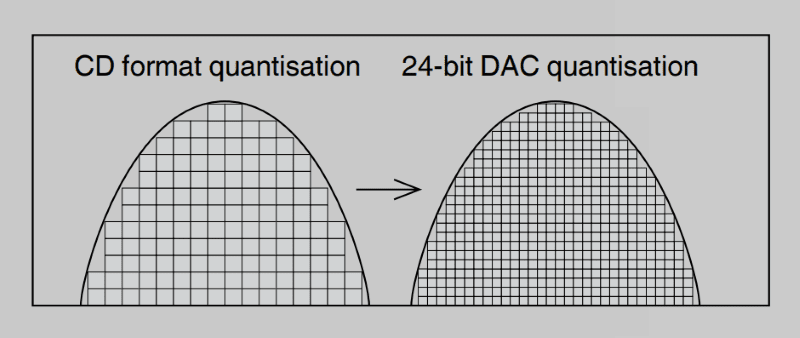
The problem is, the digital-to-analog converter doesn’t reproduce blocks. Instead, it defines an amplitude at a specific time point. A better representation of how analog waveforms are stored would be with each amplitude represented by an infinitely thin vertical line.
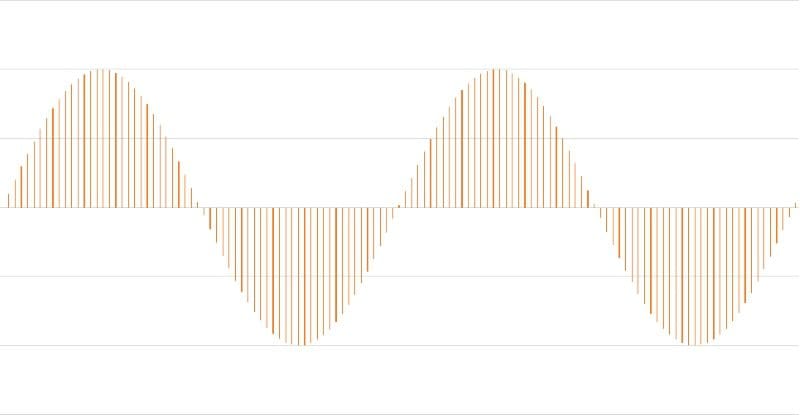
A better way to describe the function of a DAC is to state that each sample has a specific voltage at a particular point in time. The DAC has a low-pass filter on its output that ensures that the waveform flows smoothly to the next sample level. There are no steps or notches, ever.
Digital Bit Depth Experiment
Rather than ramble on about theory, let’s fire up Adobe Audition and do a real-world experiment to show the difference between 16- and 24-bit recordings. We’ll use the standard compact disc sampling rate of 44.1 kHz and a 1-kHz tone. I created a 24-bit track first and saved it to my computer. I then saved that file again with a bit depth of 16 bits to ensure that the timing between the two would be perfect.
Here’s what the waveform looks like. The little dots are the samples.
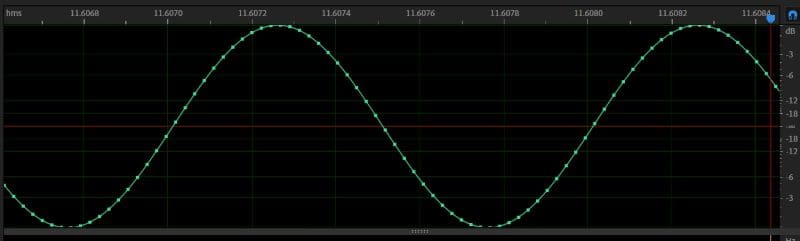
Now, I’ll load both files and subtract the 16-bit waveform from the 24-bit. The difference will show us the error caused by the difference in bit depth.
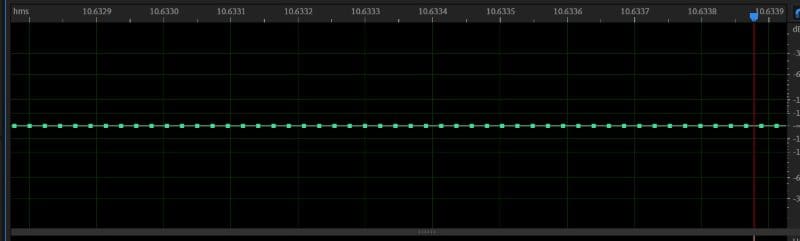
At a glance, it appears the difference is invisible. Maybe it’s hard to see the difference between the two files. Let’s look at some data in a different format. Here’s the spectral response graph of the difference.
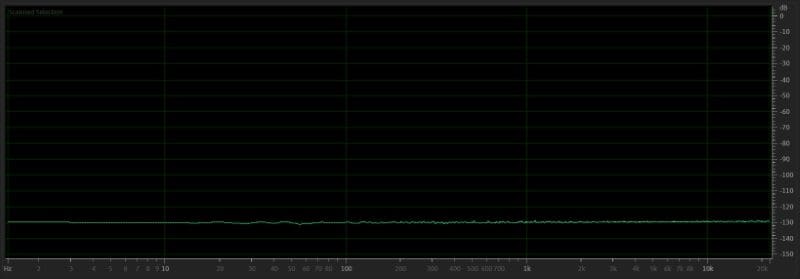
As you can see, the difference is noise at a level of -130 dB. This amplitude is WAY below the limits of any audio equipment and, as such, is inaudible.
Let’s make the comparison more dramatic, shall we? I’ve saved the 16-bit track again with a depth of 8 bits.
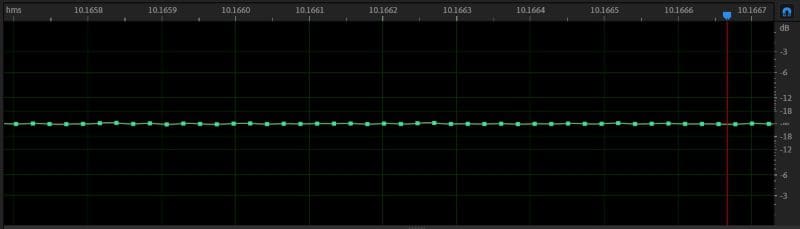
This time, we got a result. You can see some waviness in the difference. This makes sense, as an 8-bit file only has 256 possible amplitude levels, and a 1-volt waveform has a possible error of almost 2 millivolts. Let’s look at this in the spectral domain.
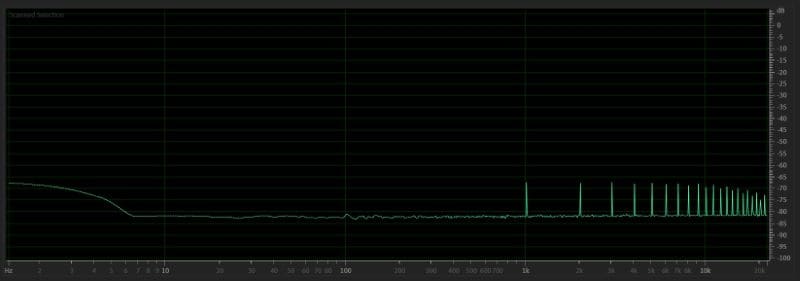
Now we have something audible. Not only can we see the 1-kHz waveform in the difference file at an amplitude of -70 dB, but we can see harmonics of that frequency at 1-kHz spacings to the upper limits of the file.
High-Resolution Audio Sounds Better
What have we learned about digital audio storage? First, each sample is infinitely small in the time domain and represents a level rather than a block. Second, there is no audible difference between a 16-bit and a 24-bit audio file. Third, 8 bits aren’t enough to accurately capture an analog waveform. What’s our takeaway? If we see marketing material that contends that a recording format with more than 16 bits of depth dramatically improves audio quality, we know it’s hogwash.
Wait, what about hi-res audio? Doesn’t it sound better than conventional CD quality? The answer is often yes. The reason isn’t mathematical, though. Sampling rates above the CD standard of 44.1 kHz can capture more harmonic information. Is this audible? Unlikely. Does having more than 16 bits of depth help? We’ve proven it doesn’t. So, why do hi-res recordings often sound better than older CD-quality recordings? The equipment used in the studio to convert the analog waveform from a microphone is likely decades newer and adds less distortion to the signal. If the recording is genuinely intended to be high-resolution, the quality of the microphone itself is better. Those are HUGE in terms of quality and accuracy.
A second benefit of higher bit-depth audio files is less background noise. When multiple sound samples are combined in software like Pro Tools, the chances of the background noise combining to become an issue are dramatically reduced.
The next time you shop for a car radio, consider a unit that supports playback of hi-res audio files. They sound better and will improve your listening experience. A local specialty mobile enhancement retailer can help you pick a radio that suits your needs and is easy to use.

