Over the past few years, I’ve written several articles about harmonic distortion. While ideally they’re pretty clear in their message, I might have jumped over the need to define the term harmonic itself. So, let’s look at what harmonics are in terms of audio signals.
What Are Harmonics?
In reference to music, the Oxford English Dictionary defines the word harmonic as “an overtone accompanying a fundamental tone at a fixed interval, produced by the vibration of a string, column of air, etc., in an exact fraction of its length.” That fraction of length (1/2, 1/3, 1/4, etc.) results in multiples (2, 3, 4, etc.) of the fundamental frequency.
If we play a note on a piano, middle C, for example, the strings on the piano are tuned to resonate at a frequency of 256 Hz (or somewhere between 256 and 280 Hz). What gives a piano a different sound than a guitar or upright bass playing the exact same note is the harmonic content of the played sound. A pure, computer-generated tone of 256 Hz would look like the image below when viewed in the frequency domain.
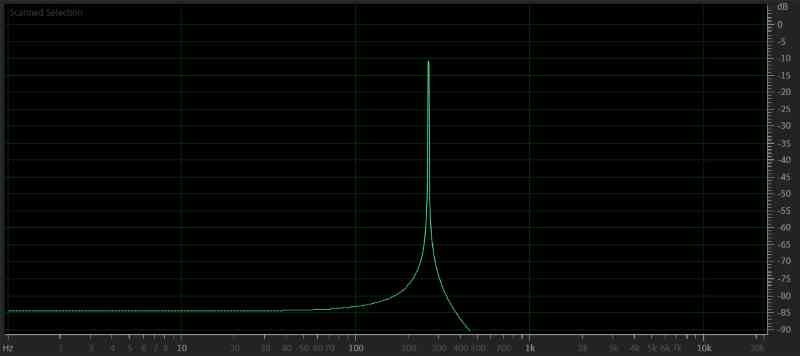
As you can see, there is no other information of significant amplitude in the file. This purity doesn’t happen in the real world. So I searched the internet for a recording of a tuning fork – something that I felt would produce the purest single tone. This particular tuning fork resonates at a frequency of 515 Hz. The averaged frequency response of the recording is shown in the image below.
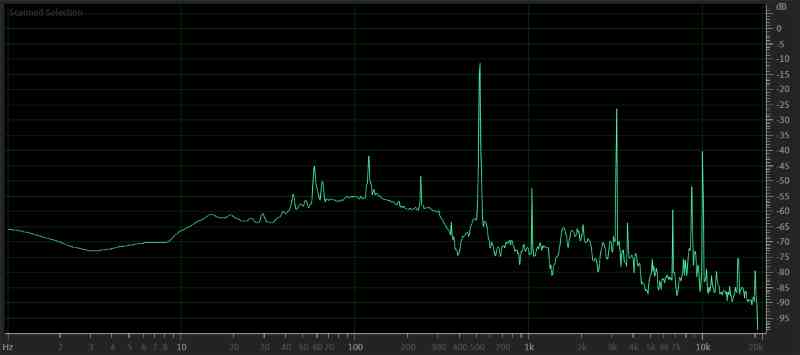
If we look at the peaks in the recording, we can see the fundamental at 515 Hz at a level of -11.34 dB FS. We can also see a second loud peak at 3100 Hz at a level of -26.36 dB FS. This second peak would be clearly audible in the playback. There’s a third loud peak around 9775 Hz at a level of -40.51 dB FS. At about 39 dB below the loudest peak, this would be harder to hear but would still be audible.
Let’s do some simple math. The 3100 Hz peak is at six times the frequency of the 515 Hz fundamental. The 9775 Hz peak is 19 times the fundamental, making it the 19th harmonic.
Harmonics are multiples of a fundamental or base frequency. If we have a 256 Hz tone, the second harmonic would be at 512 Hz, the third would be 768 Hz, and the fourth would be 1024 Hz. Harmonics can continue well beyond the range of recording equipment and our ears’ ability to detect high-frequency sounds, often at much lower levels.
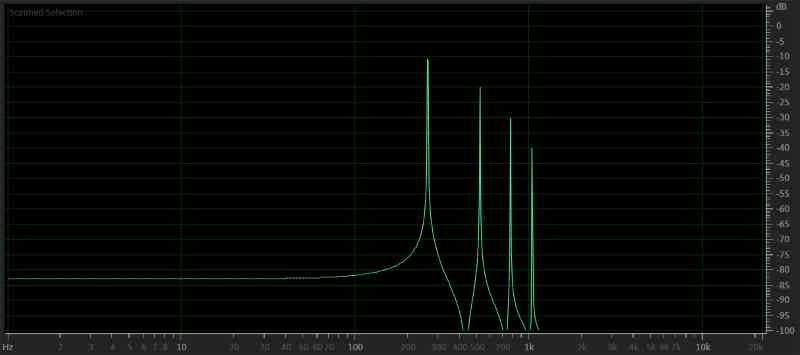
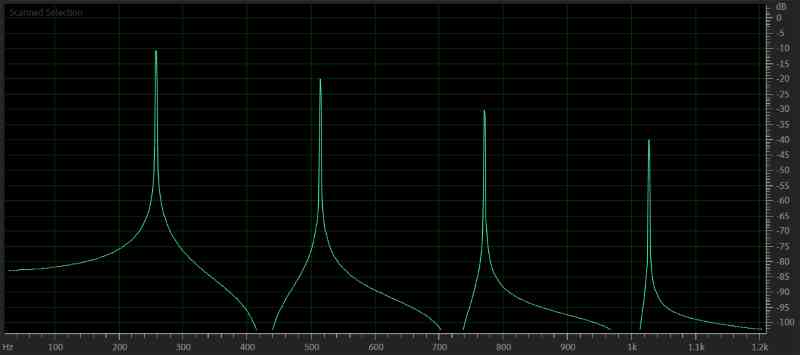
In all the graphs so far, I’ve used the conventional logarithmic scale for the X-axis. To help make the concept of harmonics and multiples of a specific frequency clearer, let’s look at a zoomed-in selection of the above graph but switch to a linear frequency scale for the X-axis. Pay close attention to the numbers on the bottom of the graph and compare them to the one above. They are the same. The linear scaling helps to display the even spacing between the tones better.
Harmonics in Music
Ok, let’s circle back to our first discussion of a piano and middle C. I downloaded a royalty-free recording of someone playing middle C on the piano so we could analyze it in Adobe Audition. The averaged frequency information is in the image below.
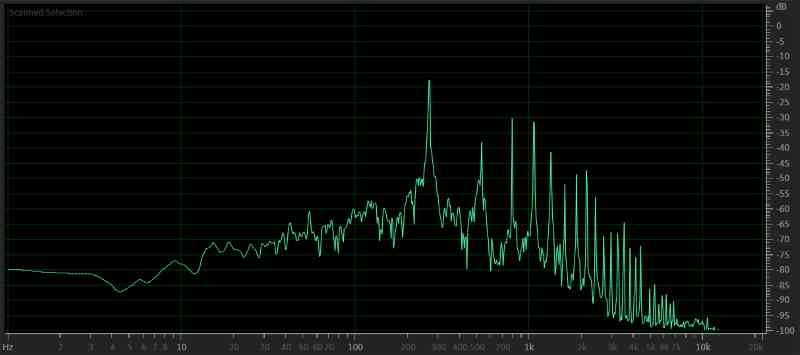
We can see that middle C on this piano is tuned to 262 Hz. The second harmonic is right at 524 Hz, the third at 786 Hz, the fourth at 1048 Hz, etc. So this single note on the piano, with information at the top of what would be considered the midbass region, has harmonic information that extends below 2.5 kHz. That’s into the range of some tweeters. The harmonics’ amplitude makes a piano sound the way it does.
Let’s look at another instrument. I’ve downloaded a sampling of a trumpet playing the same C note. The frequency information is in the image below.
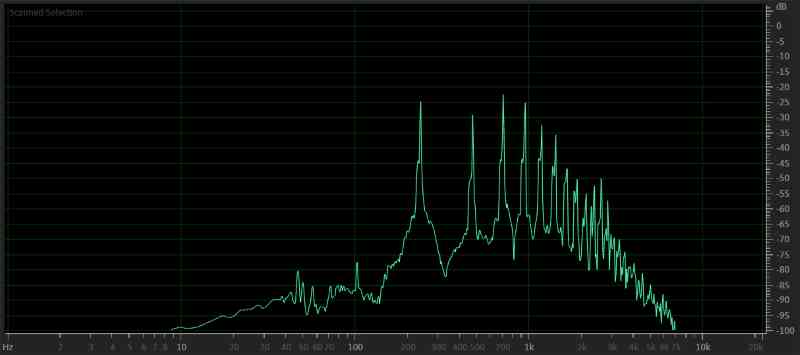
In the above frequency analysis, we can see the fundamental at 233 Hz, the first harmonic at 466 Hz, the third at 699 Hz and so on. So again, there is essential audio information from this single note past 2.5 kHz.
Why Harmonics Matter
These two examples explain how the sounds we hear contain harmonics and highlight the importance of reproducing midbass, midrange and high-frequency information with even balance. Even the slightest dip can affect the sound of an instrument or voice. Getting this right requires a properly designed audio system with expert digital signal processor calibration. Drop by your local specialty mobile enhancement retailer to learn more about how you can upgrade the sound system in your car or truck to reproduce music with impressive accuracy.

