Car audio upgrades are much more complex than setting up speakers in your living room. They are, unless all you have in the system is a set of coaxial speakers in your doors. Your installer has to consider crossover slopes and alignments if you have front and rear speakers and a subwoofer. They must also understand how the settings interact at the crossover frequency. Let’s take a nerdy look at crossover slopes and alignments, and how they sum together.
Why Do Speakers Need Crossovers?
We primarily use crossovers on speakers to protect smaller drivers from damage from over-excursion and overpowering. Say your car audio system has a set of 1-inch tweeters in the dash or the doors. Those small drivers can’t produce bass frequencies with any efficiency, and they can only a handle few watts of power. Yes, we know they say 80, 100 or 150 watts on them. But that’s their rating with pink noise referenced to bass frequencies. When you filter out everything below 3,000 Hz, all that’s left of a 100-watt signal is about 0.26 watt for the tweeter. Feeding it a sine wave at 100 watts will destroy it in about a second.
The second reason we use crossovers is to prevent excursion damage. Can you imagine sending 100 watts of deep bass information into a 3.5-inch dash speaker or a PA-style midrange? With only a few millimeters of excursion capability, these small speakers will be pushed well beyond their linear excursion limits, adding significant distortion to the output. Think of it like mechanical clipping. It sounds terrible and can damage the suspension and voice coil. High-pass crossovers are the ideal solution for preventing the above issues.
Low-pass crossovers are needed to ensure that the output from the speaker system comes from a single source. You would never want a midrange driver playing up to 5 kHz when the tweeter is playing from 3 kHz and up. The goal of the low-pass crossover on a midrange or woofer is to keep the transition from one speaker to the other smooth and transparent.
Crossover Slopes and Output Attenuation
Crossovers don’t stop all sound reproduction above or below a specific frequency. For example, a tweeter still produces audio information at 2 and 2.5 kHz when set up with a 3-kHz high-pass crossover. If you look at the graph below, you’ll see a -6 dB/octave high-pass crossover set at 3 kHz.
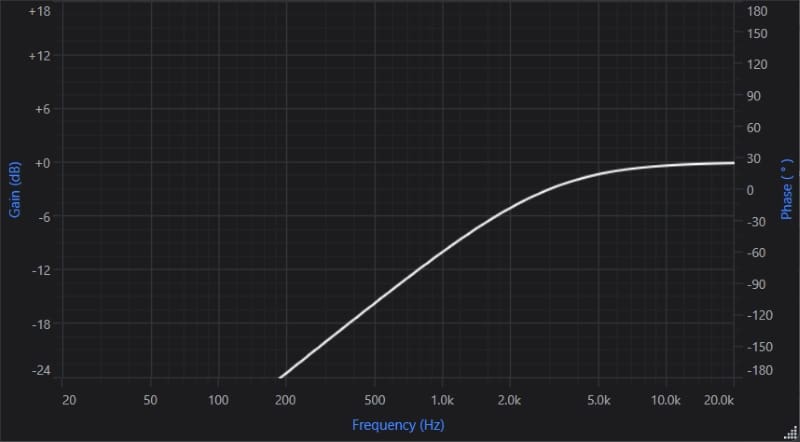
If we analyze the information carefully, we can see that the output from this ARC Audio digital signal processor would be at -3 dB at the crossover frequency of 3 kHz. The frequency set in the software can be called the crossover frequency or the knee frequency. Looking farther to the left, the output decreases with frequency. The difference between 3 kHz and 2 kHz is 6 dB. The difference between 2 kHz and 1 kHz is another 6 dB. The rate at which the output gets quieter is called the crossover slope. In this example, it’s -6 dB per octave. This is also known as a first-order crossover.
Digital signal processors have made it easy for installers to set crossovers quickly and accurately. Entering a value into software is much more precise than turning a knob on an amplifier. Those knobs are connected to potentiometers (adjustable resistors) that are notoriously inconsistent. Some companies used resistor networks instead of potentiometers on their electronic crossovers, like AudioControl’s infamous 24XS.
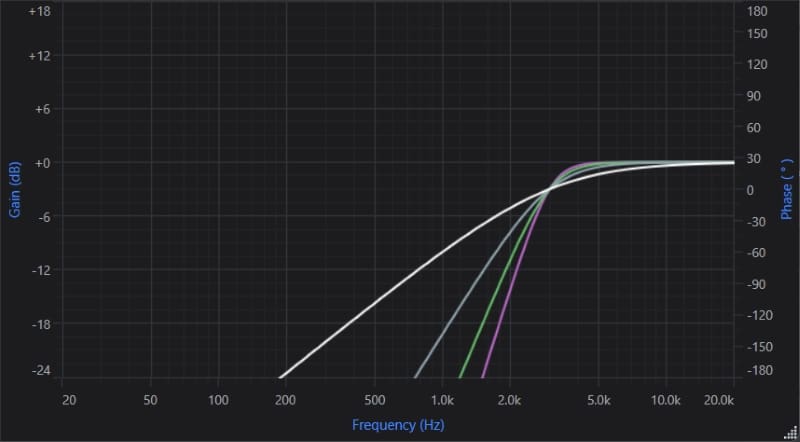
The image above shows our original first-order, -6 dB/octave high-pass filter in white. The gray trace is a -12 dB/octave second-order filter. The green trace is a third-order, -18 dB/octave filter. Finally, the violet trace is a fourth-order, -24 dB/octave high-pass filter.
The benefit of steeper filters is improved signal attenuation at lower frequencies. The first-order filter was down 10 dB at 1 kHz. This amplitude means the speaker would get 1/10 as much power as it does through the pass band (frequencies above the crossover point). The second-order filter results in the signal at 1 kHz being -19.2 dB down. That’s close to 1/100 the power at 1 kHz compared to above 3 kHz. The third-order filter is down 28.7 dB, and the fourth-order is -38.2.
A second benefit of steeper filters is that the range of frequencies where the output comes from both drivers simultaneously is much smaller.
Crossover Alignments
So far, we’ve been looking at a crossover with a Butterworth response. Originally, crossovers were constructed using capacitors, inductors and resistors. Balancing the attenuation rate while delivering flat performance through the pass band (the range of frequencies you want to hear) was tricky with off-the-shelf passive components, even in electronic circuits. Butterworth filters offer moderate roll-off rates but deliver smooth response through the pass-band. They also have an output level of -3 dB at the crossover frequency. This level at the crossover frequency is a crucial consideration that we’ll circle back to later.
Another commonly available crossover type is called a Bessel alignment. Bessel filters offered the best group delay, whereas the Butterworth had the smoothest pass-band response characteristics. These are also popular in audio systems. We’ll get into a deep discussion of group-delay another time. For now, think of it like “timing issues.” Bessel filters are very similar to Butterworth in that they have a -3 dB level at the crossover frequency. Bessel filters are only available in even-order alignments, so second-order -12 dB/octave or fourth-order -24 dB/octave in most systems.
The last filter we’ll talk about is called the Linkwitz-Riley. This is another filter option that’s only available in even-order alignments. Technicians designing electronic circuits can create a Linkwitz-Riley (LR) filter by combining two Butterworth filters. So, a second-order LR (LR2) is two first-order Butterworth filters added together in series. An LR4 is two second-order Butterworth filters. The key benefit of the Linkwitz-Riley filter is that the output is at -6 dB at the crossover frequency.
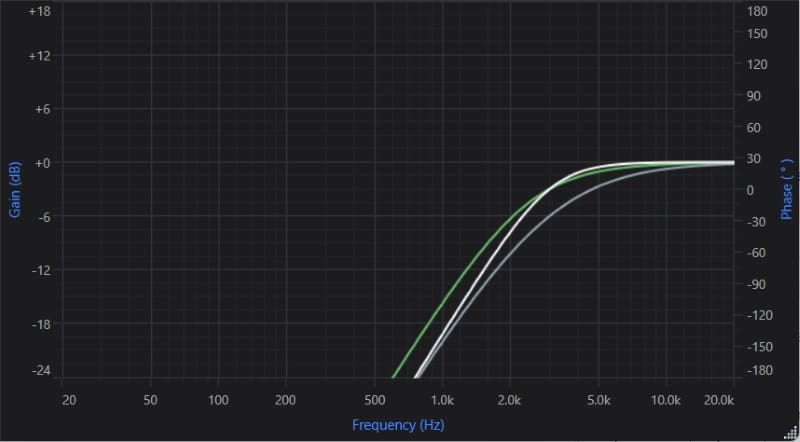
The image above shows a Butterworth alignment in white, a Linkwitz-Riley alignment in gray and a Bessel alignment in green.
Speakers and Signal Summing
Two identical speakers playing the same signal at the same amplitude, at equal distances from the listener, will produce 6 dB SPL more output than a single speaker.
Producing smooth frequency response through the crossover region is crucial for configuring and calibrating car audio systems. If the crossovers you’ve chosen have a -3 dB level at the knee frequency (the frequency set in the software), then the output of the two speakers sums to produce a bump that’s +3 dB in amplitude. This is a problem. We don’t want bumps in frequency response anywhere in the system. The high- and low-pass signals sum flat if your installer uses a Linkwitz-Riley filter at -6 dB at the crossover point. As a result, the system is much easier to equalize, and there’s a reduced overlap range between the two drivers.
If you look at most car audio amplifiers with built-in crossovers, you’ll find that entry- to mid-level models offer -12 dB/octave Butterworth crossovers. As you move up in the model ranges, you might find they have -18 or -24 dB/octave filters. Very few amplifiers with built-in electronic crossovers offer Linkwitz-Riley alignments.

Setting Electronic Crossovers
Let’s discuss setting a crossover on an amplifier between a subwoofer and the door speakers. In almost all instances, assuming the door speakers can play loudly and at midbass frequencies, the optimum crossover point is usually 80 Hz. Regarding the crossover slope, you want it to be as steep as possible, up to -24 dB/octave.
If a technician eyeballs the crossover options on an amplifier and tries to set them both to that frequency, we run into several problems. First, the actual crossover frequency is likely quite different than the labels on the amp chassis because of variances in the potentiometer inside the amp.
Next, even if the labels were perfect, unless the electronic crossovers have a Linkwitz-Riley alignment, the system’s output will have a 3 dB bump at the crossover frequency. We must underlap the crossovers when they are Butterworth or Bessel alignments. This makes using a real-time analyzer the only accurate way to set this type of electronic crossover.
Adding a high-quality digital signal processor to the system is a more straightforward and predictable solution. Your installer can select Linkwitz-Riley filter alignments and make precise crossover frequency selections. Of equal importance, they can then use a calibrated microphone to adjust the frequency response of the system to compensate for reflections and resonances in the vehicle. Drop by a local specialty mobile enhancement retailer today to discover the digital signal processors that are available to upgrade your system.

