Our Car Audio Masterclass series offers a comprehensive introduction to the essential concepts of car audio systems, covering everything from basic terminology to advanced measurement techniques. To learn more, check out the other articles in the series:
- Car Audio Masterclass 101.1 – Audio Basics: Learn key audio terms and concepts.
- Car Audio Masterclass 101.2 – Understanding Basic Electricity: Explore voltage, current, and resistance.
- Car Audio Masterclass 101.3 – Electric Circuits: Understand series and parallel circuits.
- Car Audio Masterclass 101.4 – Magnetism: Discover the role of magnetism in speakers.
- Car Audio Masterclass 101.5 – Direct and Alternating Current: Compare DC and AC currents.
- Car Audio Masterclass 101.6 – AC Calculations: Dive into AC waveform calculations.
- Car Audio Masterclass 101.8 – Speakers, Power, and SPL: Understand speaker power and sound levels.
- Car Audio Masterclass 101.9 – Time and Frequency Domain Measurement: Explore frequency and time measurements.
- Car Audio Masterclass 101.10 – Digital Multimeter: Learn to use a multimeter in car audio.
We need to understand a bit more terminology before applying our knowledge to how car audio components work. In this Car Audio Masterclass lesson, we will talk about the decibel. We use this term in the context of audio systems in two ways, so we’ll split them up to avoid confusion. This one will get a bit nerdy, but we need to cover this for further discussions to make any sense.
What is a Decibel?
In both science and nature, we often discuss values that vary over a wide range. Decibels compress large ratios into much more manageable numbers. Specifically, a decibel represents a ratio between two numbers. For example, if we want to quantify the noise an amplifier adds to an audio signal, we might measure the peak noise amplitude at 0.00000562 volts, whereas the stimulus signal might be 2 volts. We can express the ratio between these two numbers using decibels.
The formula to convert a voltage ratio to decibels is dB = 20 log(V1 ÷ V2). This works out to -111.03 dB. This ratio presentation provides the same information but is more straightforward than saying something like 0.000281%.
What Is This Logarithmic Stuff?
You will note that we used the mathematical operation logarithm above. Taking the logarithmic transformation of two numbers is the same as asking, “To what power must a given base be raised to produce this number?” We use a base numbering system of 10 for everything audio-related. For instance, if something has a logarithmic ratio of 3, the ratio is the same as 10 to the power of 3. Ten to the power of 3 is 1,000. Thus, log10(1000) = 3. We would read the latter as “the base 10 log of 1000 equals three.” Based on this, we can predict that log10(100) is 2 and log10(10,000) is 4.
We can plot logarithmic numbers on a chart to help present their ratio visually. Let’s look at some ratios between 0 and 200.
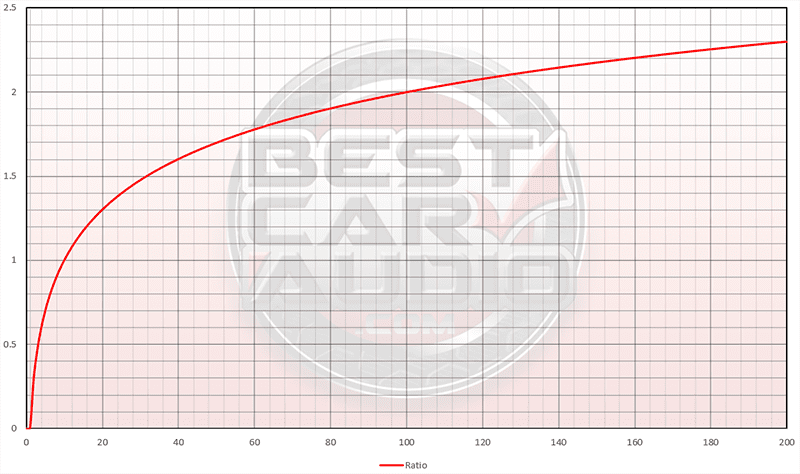
If we look at the chart, we can see a few interesting pieces of information. First, the log of 2 is 0.30103. The log of 10 is 1. The log of 20 is 1.30103. The log of 40 is 1.60206. The log of 100 is 2. You will see this 0.30103 value and multiples of it come up repeatedly in ratio comparisons.
Power and Amplitude Unit Math
Any time we want to compare two widely different values, we can use decibels. The math changes slightly depending on whether we compare power or amplitude units. For voltage comparisons, the formula is 20 times the log of the ratio between the values. We use a factor of 20 instead of 10 because these quantities (voltage, sound pressure, current, acceleration, and magnetic field strength) are related to power, and power is proportional to the square of the amplitude of these quantities.
When we compare two power levels, the formula is 10 times the log of the ratio between the values. For example, if we want to describe how much power a large amplifier can produce, we can compare the output to a reference. In this example, the unit dBW, or decibel watts, compares an output of 977 watts to 1 watt. So, our 977-watt example is equivalent to 29.9 dBW. We use these numbers in our Test Drive Reviews and wattage measurements to indicate an amplifier’s capabilities.
Using the dBW unit makes it easy to see how little effect small changes in power at high output levels will have on audio system performance. For example, if one amplifier produces 977 watts, which is equal to 29.9 dBW, and a second amplifier produces 1077 watts, that’s 30.31 dBW. The difference between the two is only 0.41 dBW. This means the 1077-watt amplifier would produce sound only 0.41 dB SPL louder than an amplifier delivering 977 watts, assuming a linear response from the subwoofer.
Voltage Ratios
As mentioned, the math when calculating the ratio between voltages is 20 log(V1 ÷ V2). The unit dBV, decibel volts, uses a V2 value of 1 volt. So, if we measure the output of an amplifier to be 9.2 volts, that’s equal to 19.276 dBV.
We use 20 log(V1 ÷ V2) when comparing current, voltage, and sound pressure levels.
Power Ratios
Although we just covered the math above, we’ll reiterate it as a reference. The math to compare two power levels is 10 log(P1 ÷ P2). If we want the answer in decibel watts or dBW, we use one watt as P2. An output of 1500 watts is equivalent to 31.76 dBW.
We use 10 log(P1 ÷ P2) when comparing power levels in watts.
Audio-Specific Units
Suppose you are old enough to have recorded music on a cassette tape or been in a recording studio. In that case, you might have seen analog or digital level meters showing the amplitude level. These meters are often calibrated in dBU and are called Voltage Unit meters. A voltage unit is a term left over from the days of the telegraph and represents one milliwatt into a 600-ohm load. This also happens to be 0.775 volts RMS. So, if you see a VU meter at 0 dB, you know there is 0.775 volts of signal. Is this useful in modern recording? That’s a whole other matter. However, they are great for ensuring the left and right channels are at the same amplitude.

The dBm is another unit you might see when looking at radio frequency transmission specifications. This is the measure of radio frequency signal strength. The dBm is a ratio of signal power referenced to 1 milliwatt. So, 10 dBm is 10 milliwatts, and 20 dBm is 100 milliwatts.
A similar unit that’s more common in car audio systems is the dBf. This is also a unit of RF signal strength, but it’s referenced to a femtowatt. One femtowatt is 10^-15 watts. A radio tuner might have a sensitivity rating of 7 dBf. This means it can lock on to a radio station signal that the antenna picks up if it’s at 7 dBf or higher.

Sound Pressure Levels
As discussed in the first lesson, we use the unit decibel to describe how loud a speaker might be playing. To summarize, the unit we use is dB SPL. The SPL suffix denotes that we are talking about sound pressure levels.
To extend our discussion about decibels, 0 dB SPL is equal to 20 micropascals. Without regurgitating all the science, 20 micropascals of air pressure change is considered the quietest sound humans can detect. It takes relatively massive changes in air pressure to produce what we consider to be a louder sound. For example, 200 micropascals is 20 dB SPL. A sound pressure of 20 dB SPL is still very quiet. If you are sitting in a room with a fan running, the sound level might be 50 dB SPL. That’s equivalent to 6324.6 micropascals. This is a perfect example of numbers getting too large quickly. Using a logarithmic decibel scale simplifies describing how loud something is. Nobody wants to go to a rock concert and claim, “Oh man, that Foo Fighters concert felt like 6,324,555 micropascals loud!”
Ratios
The last item we will discuss is simple level ratios. If you look at the tuner specifications above, you can see that the radio has a channel separation specification of 45 dB. This number describes the isolation or leakage from one channel to the other. If there were a signal at 80 dB on one channel, that signal would appear on the other as 35 dB. The math is simple: 80 – 45 = 35.
We often use logarithmic ratios to describe noise levels or crosstalk. For example, a good quality car audio amplifier might have a signal-to-noise ratio (SNR) of 80 dB at a specific output level. Including the output level is crucial. So, if the output of an amplifier is 1 watt into a four-ohm load (which equals two volts), and the SNR is 80 dB, then the amp adds 0.0002 volts of noise. Less noise is always better, but this is a good number.
Understanding Decibel Ratios
This is a lot of information to take in, but understanding decibel ratios is crucial for understanding specifications and measurements in audio equipment. The key takeaway is that decibels are an efficient way to compare large ratios while keeping numbers manageable. In the next lesson, we will expand on sound pressure level discussions and look at how changes in power and speaker quantity affect a system’s output.

